W poprzednim wpisie ‘Statystyka z Tableau- podstawawy’ poznaliśmy podstawowe miary statystyczne – średnią, medianę, minimum i maksimum, kwartyle, percentyle oraz rozstęp ćwiartkowy. Nauczyliśmy się przedstawiać je na wykresach przy użyciu funkcjonalności Tableau takich jak linie referencyjne oraz wykorzystywać w funkcjach jako pola obliczeniowe. W poniższym wpisie pójdziemy krok dalej i poznamy więcej miar statystycznych: wariancję i odchylenie standardowe oraz poznamy kiedy stosować które miary.
Statystyka z Tableau- mierzymy rozrzut wartości – wariancja
Oprócz podstawowych miar statystycznych jak średnia określających dane zjawisko istotne jest zrozumienie zmienności. Aby lepiej to zobrazować, wróćmy do przykładu z poprzedniego wpisu – zarobki pracowników. Tym razem porównamy zarobki w dwóch działach, które mają taką samą średnią:
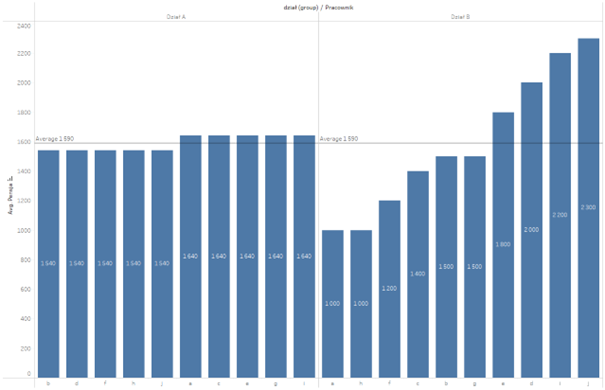
Jak widzimy na wykresie, pomimo identycznej średniej, rozkład samych wartości wynagrodzeń jest zdecydowanie różny w obu przypadkach. Po to właśnie wprowadzamy pojęcie zmienności, a dokładniej mówiąc – wariancji. Wariancja mierzy odchylenie wartości od średniej. Najprościej byłoby to zrobić jako różnicę dla każdego punktu i następnie zsumować powstałe w ten sposób wartości:
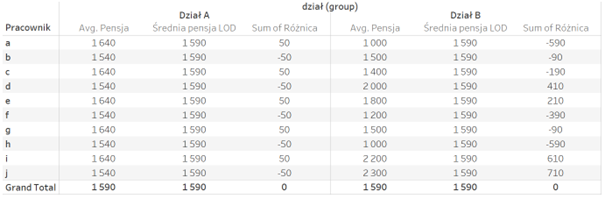
Problem oczywiście jest taki, że sumując różnice pensja vs średnia zawsze wyjdzie nam zero – część wartości jest powyżej a część poniżej średniej. Stąd wprowadzono podniesienie tak uzyskanej różnicy do kwadratu, aby zlikwidować problem przeciwnych znaków. Dzieląc tak uzyskaną wartość przez liczbę obserwacji, uzyskujemy wariancję:
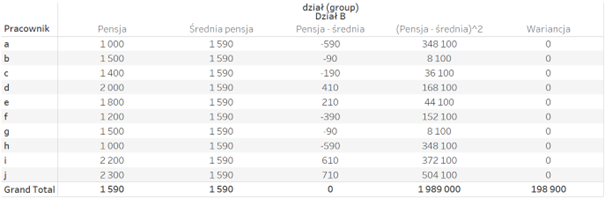
Bardziej intuicyjna miara zmienności – odchylenie standardowe
Aby nieco ułatwić interpretację wariancji, która stanowi różnicę podniesioną do kwadratu, często stosuje się odchylenie standardowe – czyli pierwiastek z wariancji:
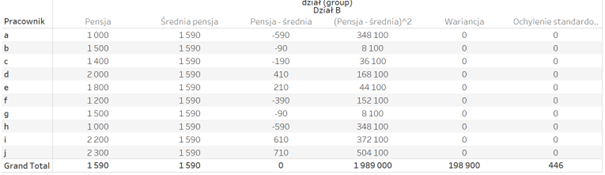
Tym samym możemy zinterpretować nieco łatwiej dane – wynagrodzenie wynosi średnio 1590 z odchyleniem 446. Wróćmy do naszego porównania dwóch działów – gdzie w obu przypadkach średnia pensja była taka sama:

Tym razem odchylenie standardowe wskazuje w którym przypadku zmienność wynagrodzeń jest większa a w którym mniejsza. O to nam chodziło.
Statystyka z Tableau- miary zmienności jako pola obliczeniowe i elementy na wykresie
W poprzednim akapicie liczyliśmy wariancję i odchylenie standardowe ‘na piechotę’, natomiast możemy wykorzystać wbudowane funkcje statystyczne w Tableau do kalkulacji tych miar. Funkcje te to:
– VAR ([Miara]) – wariancja próbki, VARP ([Miara]) – wariancja populacji
– STDEV ([Miara]) – odchylenie standardowe próbki, STDEVP ([Miara]) – odchylenie standardowe populacji
Tak stworzone miary możemy wykorzystywać w analizach jako pola obliczeniowe:

Tableau to oczywiście analityka wizualna więc nie mogło zabraknąć graficznej prezentacji tych miar. Możemy wykorzystać odchylenie standardowe do prezentacji rozkładu danych wykorzystując funkcjonalność Distribution Band z zakładki Analytics:
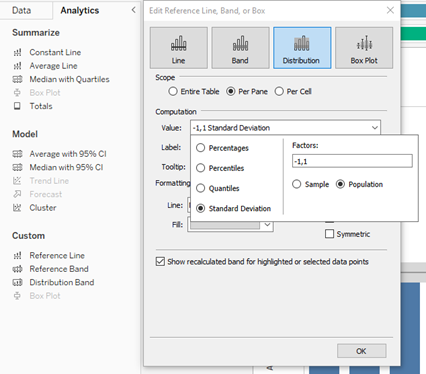
Po wybraniu Distribution Band wybieramy w liście Value: Standard Deviation (domyślnie +-1), zaznaczamy Sample (gdy mamy próbkę danych) lub Population (gdy mamy wszystkie dane) i gotowe:
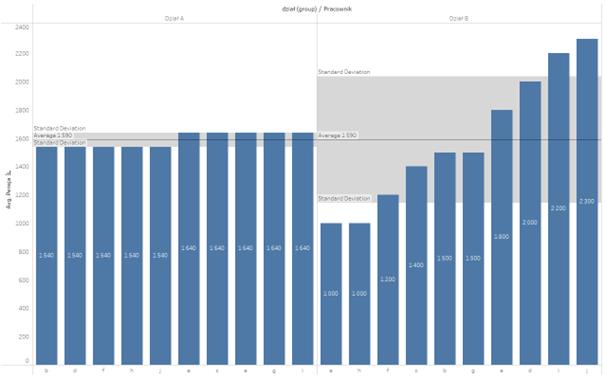
Szare zakresy prezentują obszar od średnia minus odchylenie standardowe do średnia plus odchylenie standardowe. Widać na wykresie jednoznacznie, który zestaw danych ma większą zmienność.
Statystyka z Tableau- na co musimy uważać w analizie zmienności
W poprzednim wpisie wskazywałem, że w przypadku zbioru danych z wartościami odstającymi miary takie jak średnia mogą być nie do końca reprezentatywne i zaburzać obraz. Podobnie jest z odchyleniem standardowym, które również jest miarą klasyczną. Wróćmy do przykładu pensji, ale dodajmy wysoką pensję pracownika x:
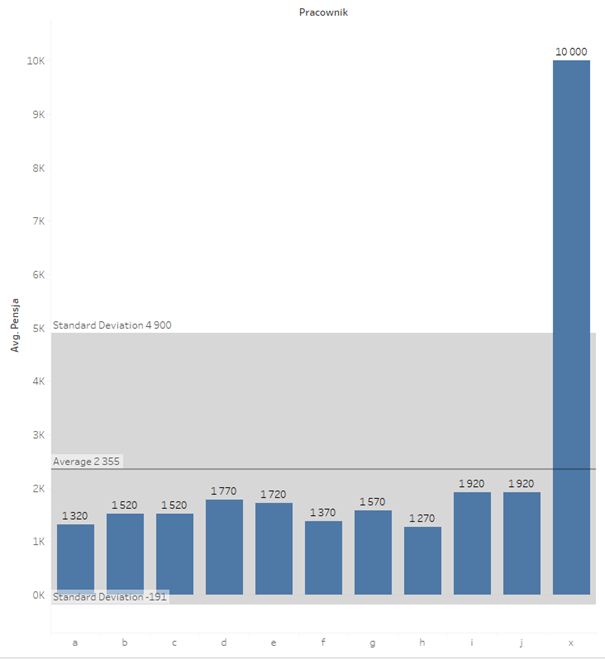
Jak widać odchylenie standardowe wyskoczyło nam w kosmos. Mówiąc teraz, że wynagrodzenie wynosi średnio 2355 +- 2546 nie wiele nam mówi, zwłaszcza że wynagrodzenie raczej nie może być na minusie. Co w takim przypadku? Cóż, najlepiej przejść do miar pozycyjnych – mediana zamiast średniej oraz rozstęp ćwiartkowy zamiast odchylenie standardowego. Przypomnijmy z poprzedniego wpisu – mediana to wartość środkowa, od której tyle samo punktów danych jest większych i mniejszych. Rozstęp ćwiartkowy to różnica pomiędzy górnym a dolnym kwartylem, w ramach którego zawiera się 50% naszych danych. Wizualnie w Tableau możemy dodać odpowiedni zakres z zakładki Analytics, wybierając Median with Quartiles:

Efekt na wykresie – widać że dużo lepiej pokazuje rozkład niż średnia/odchylenie standardowe:
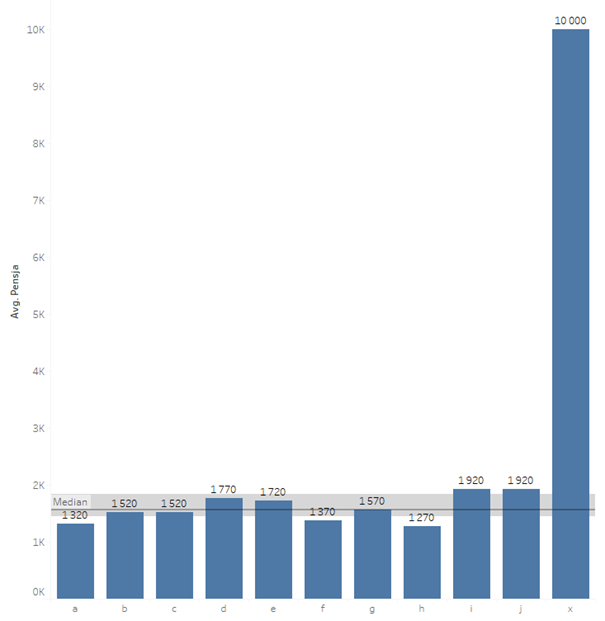
Podstawowe statystki są istotne
Zaczynając analizę danych, warto rozpocząć od podstawowych statystyk. Pozwolą one zbudować podstawową wiedzę na temat danych i mogą wskazać kierunek analizy. Należy przy tym pamiętać o ograniczeniach – przykładowo przy średniej, która jest wrażliwa na wartości odstające. Jeżeli średnia bardzo różni się od mediany to możemy spodziewać się istotnych wartości odstających. Warto wtedy odstąpić od miar klasycznych i przejść w kierunku miar pozycyjnych. Tableau wesprze nas tutaj zarówno przy kalkulacjach (dzięki wbudowanym funkcjom statystycznym) jak i w aspekcie wizualnym (za pomocą linii referencyjnych, rozkładów dystrybucji czy box-plotów).
Autor: Mateusz Karmalski Tableau Author
